The Crystal Structure of Alamosite, PbSiO₃ ¹

Abstract

Alamosite, PbSiO₃, has space group P2 In with cell parameters for the reduced cell a = 11.23Å, b= 7.08Å, c = 12.26Å, and ß = 113°15´, with Z= 12. The structure has been determined using three-dimensional counter diffractometer data. Refinement converged with R = 11.1%, including a number of reflections omitted due to extinction effects. The structure of alamosite is unique in that it consists partially of chains of tetrahedra extending parallel to [10¯1] with a lattice translation repeat of twelve tetrahedra. The three independent Pb atoms are coordinated by 3 or 4 oxygen atoms, in each case the nearest oxygen neighbors being distributed on one side of the Pb atom, indicating covalency in Pb-O bonding. The Pb atoms and their coordinating oxygen atoms are related by an approximation to a 3₁ screw axis parallel to [010] so that they form a continuous spiral of bonded Pb, O atoms.

Introduction

Mackay (1952) determined that alamosite, PbSiO₃, has space group P2/c or Pc, and unit-cell parameters a = 11.28Å, b = 7.08Å, c = 13.06Å, and ß = 120°. Following the suggestion of Palache and Merwin (1909), he compared the properties of alamosite with those of the monoclinic form of CaSiO₃, parawollastonite, for possible evidence of isotypy. The lack of correspondence suggested a difference in structure. The 3: 1 ratio of O: Si indicates that alamosite should have a structure based on a silicate chain or ring. Mackay noted that the presence of rings is more probable since alamosite has a pseudo-hexagonal cell and indices of refraction indicating "anisotropic structure units." Prewitt and Peacor (1964), in a review of chain metasilicate structures, showed that such structures with cations larger than Ca, such as Pb, were unlikely to be based on silicate chains.

Unit cell and space group

Specimens of alamosite from Alamos, Sonora, Mexico were kindly provided by Dr. C. Frondel from the Harvard mineralogical collection, catalogue number 84459. The unit-cell parameters determined for this material are a = 11.23Å, b = 7.08Å, c = 12.95Å, and ß = 119°34´. Systematic extinctions were found which verified that alamosite has space group P2/c or Pc, as determined by Mackay. The cell parameters for the P2/n or Pn setting have been used throughout our results, however, since this corresponds with the reduced cell. Parameters for this cell are a = 11.23Å, b = 7.08Å, c = 12.26Å, and ß = 113°15´. Mackay noted that a test for piezoelectricity was negative and that many accidental absences occur on single-crystal photographs. He therefore suggested that the centrosymmetric group is probably the correct one. Mackay also determined that the calculated cell contents are 12.3 formula weights of PbSiO₃, using data of Palache and Merwin. We confirmed the value Z = 12, departures from the integral value being ascribable, in part. to error in specific-gravity determination.

Structure determination

Alamosite occurs as aggregates of radiating fibrous crystals, with fiber axis [010], and with a perfect (010) cleavage. Our type material suffered from serious lineage-structure effects with reflections broadened irregularly parallel to (010). Three-dimensional data were therefore obtained by planimetering recorded peaks, using a crystal rotated about the b axis, with CuK-alpha radiation and a scintillation counter with pulse-height analysis, followed by correction for Lorentz-polarization factors.

The function P(uw) was then calculated. From a computation of predicted relative peak heights it was clear that all peaks except Pb-Pb peaks were close to the background level. The projection symmetry was P2 with 6 PbSiO₃ per cell. No large peaks were found in special positions, so the Pb atoms were assumed to be distributed in three general positions (rank 4 in P2/n; rank 2 in this projection). Using the conjugate-peak relation (Buerger, 1959), two probable single-weight Pb-Pb inversion peaks were readily located. Each was used for the construction of an M₂(xz) function. Only three large peaks were found in this function and it was assumed that they corresponded to three Pb atoms in general positions. Structure factors were calculated on this basis and the relatively low R factor verified this decision. All attempts to locate Si and O atoms in projection through the M₄(xz), rho(xz) and Delta rho(xz) functions failed, however.

The three-dimensional Patterson function, P(uvw) was therefore calculated. The coordinates u, w of Pb-Pb vectors were known from the analyses of the two-dimensional function. Examination of P(uvw) readily resulted in identification of Pb-Pb inversion vectors, and the y coordinates of the Pb atoms were determined. Reasonable agreement between values of F_o and F_c, using only Pb atoms, verified these results. A Fourier synthesis, rho(xyz) was then prepared using those large values of F_o with signs assumed to be unambiguously determined. Only three non-equivalent peaks of approximately equal height were present with heights significantly above background, in addition to those corresponding to Pb. The cell contents are consistent with 3 Si atoms in general positions. In addition, interpeak distances were 3 ± .02Å, which is in the range of known Si-Si distances across bridging oxygen atoms. These peaks were therefore assumed to correspond to Si atoms. oxygen-atom positions were then predicted assuming ideal tetrahedral oxygen coordination about Si, on the basis that adjacent Si atoms were linked through bridging oxygens. Refinement carried out using all Pb, Si and O positions failed to converge, however. A difference Fourier synthesis Delta rho(xyz) readily suggested adjustments in some oxygen positions. Refinement was continued to convergence with R = 10.4%, excluding reflections with F_o= 0.

At this time an unusually perfect crystal of alamosite was separated which showed a major improvement over the first in perfection of reflections. The intensity data were therefore redetermined. Some crystal imperfection was still detectable in diffractometer scans however, so intensity data were again determined through the planimetering of recorded peaks. CuK-alpha radiation was again used and the data corrected for the Lorentz-polarization factor and absorption. Due to the large absorption factor, absorption had to be precisely accounted for; this was accomplished by using the IBM program ABSRP kindly provided by C. W. Burnham, taking care to define the crystal vertices to within about ± .003 mm. The crystal shape was easily defined since the crystal was a prism mounted for rotation about b and bounded by {h0l} faces and {010} cleavages, 0.17 mm long with principal diameters of about 0.06 and 0.03 mm.

Refinement was continued with the new data using the weighting scheme recommended by Cruickshank (1965), with corrections for anomalous scattering. Following convergence, with only the atomic coordinates and the single scale factor varying, it became evident that the data were subject to a secondary-extinction error, since large structure factors consistently had F₀ < F_c. Since a precise extinction correction could not readily be made, due to the complexity of the crystal shape, refinement was continued with the rejection of about 50 reflections for which a significant extinction error was indicated. The refinement rapidly converged with final cycles of refinement of atom coordinates and the single scale factor alternating

Table 1. Refined coordinates and isotropic temperature factors of alamosite (Standard deviations are given in parentheses)

Atom              x                  y                      z                       B

O(10)     .7139 (17)          .0497 (32)        .8358 (16)         .25 (29)

with cycles of isotropic temperature-factor refinement. The final values of the conventional R factor are: 11.1% including reflections with F_o= 0 and those rejected as affected by extinction; 8.7% excluding the latter; 8.3% also excluding reflections with F_o= 0. Refinement of anisotropic temperature factors was not attempted since the accuracy of the data was not sufficiently high to permit the determination of meaningful values. Values of the isotropic temperature factors and atom coordinates are given in Table 1. and of the structure factors in Table 2 (not reproduced here).

Description of the alamosite structure

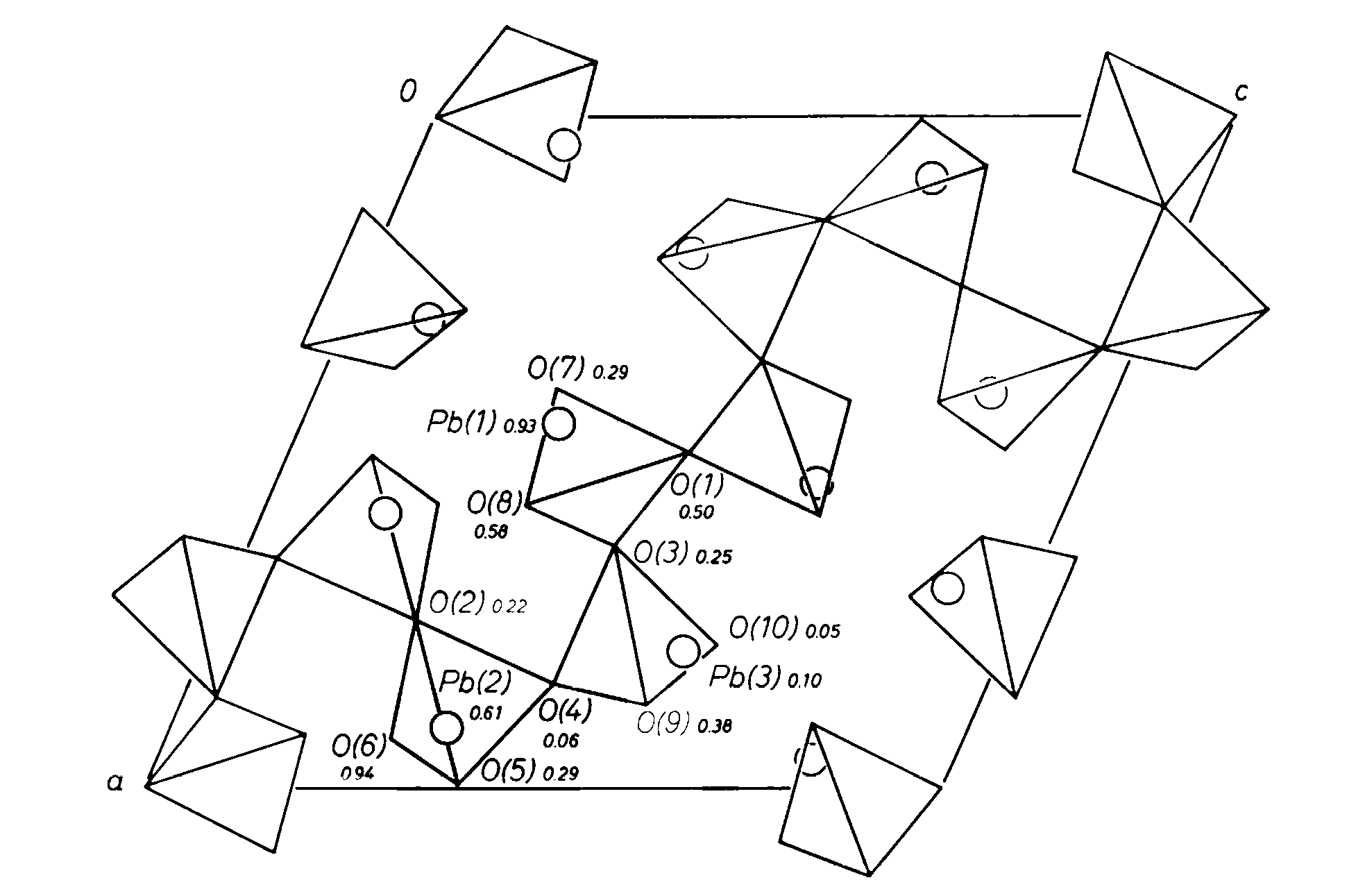
Figure 1 is a representation of the structure of alamosite projected on (010). The dominant structural feature is a chain of silica tetrahedra which extends parallel to [101]. This chain has a lattice-translation repeat of twelve tetrahedra. There are four independent bridging oxygen atoms in the chain, O(1)-O(4), with O(1)at an inversion center and O(2) on a two-fold axis. Thus, units of the chain which are three tetrahedra long form the symmetry-repeated chain unit.

Prewitt and Peacor (1964) have reviewed the general nature of metasilicate chain structures. All are based on an approximation to closest packing. No analogy to the structures of these phases (pyroxenes and pyroxenoids) is evident in the alamosite structure and thus it has a unique structural configuration.

Values of silicon-oxygen distances are given in Table 3, and values of tetrahedral oxygen-oxygen distances and oxygen-silicon-oxygen angles in Table 4. All values were calculated using the IBM program ORFEE written and kindly made available by Busing and Levy. Estimated standard deviations were calculated using the full least-squares variance-covariance matrix and estimated lattice-parameter errors. All values for the silica tetrahedra are reasonable relative to well-refined silicate structures, the range of silicon-oxygen distances being 1.60-1.67Å, that of oxygen-oxygen distances 2.59 to 2.74Å, and that of oxygen-silicon-oxygen angles 104-115°. The average of all Si-O distances is 1.628Å, while Smith and Bailey (1963) predict a value of about 1.623Å for metasilicates with no Al substitution for Si.

Liebau (1961) has reviewed the values of Si-O-Si bridging angles of silicate structures and finds that for well-determined structures they average about 140°. Major deviations from this value are unusual and therefore may indicate an error in some aspect of structure determination. Zoltai and Buerger (1959) reported an angle of 180° across a bridging oxygen of coesite, and Kamb (1960) one in zunyite. Cruickshank et al. (1962), in a detailed analysis of the thortveitite structure, confirmed that the bridging angle is 180°, as required by centrosymmetry, within the limit of accuracy of the data. The bridging angles in alamosite are: Si(1)-O(2)-Si(1), 129°; Si(1)-O(4)-Si(3), 130°; Si(2)-O(3)-Si(3), 153°; Si(2)-O(1)-Si(2), 180°. The latter value is symmetry-determined since O(1) is at an inversion center. This suggests that alamosite may not be centrosymmetric, space group P2/n, but may have one of the space groups P2 or Pn.

The relatively low R factor for a heavy-atom structure, considering especially the presence of extinction errors, indicates that alamosite is centrosymmetric within the accuracy of the data. The temperature factors for all atoms are in a range consistent with other silicate structures, with isotropic values for Pb being 0.53-0.65, for Si, 0.21-0.44, and for O, 0.23-1.49. In particular, the value for O(1) is 0.8, which is consistent with a lack of positional disorder.

The coordinations and relative spatial distributions of Pb atoms are of interest in the alamosite structure. Considering only Pb-O distances below about 2.8 (Table 3), the coordination numbers for Pb(1), Pb(2) and Pb(3) are 3, 4 and 4, respectively. The coordinating oxygen atoms are shown in Fig. 2. For each of the three Pb atoms the coordinating oxygen atoms lie to one side, with two distances in the range 2.2-2.3Å and the other one or two in the range 2.45 to 2.60Å. All other Pb-O distances are greater than 2.86Å. These coordination relations indicate that Pb-O bonds are largely covalent in nature. The structure is still consistent with charge-balance requirements for an ionic model, however. As shown in Table 5, O(1)-O(4) are each coordinated only to two Si atoms, and O(5)-O(7), O(9) and O(10) to one Si and two Pb atoms. Only O(8) shows a major deficiency in bond strength, since it is coordinated to one Si and only one Pb atom.

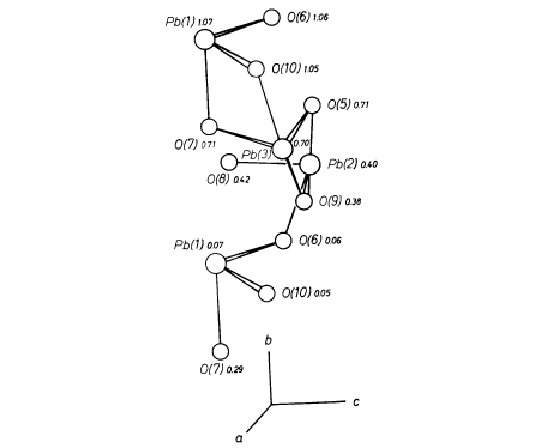Fig. 2. Orthographic projection of the Pb-O polyhedra. The larger circles represent Pb, and the smaller oxygen. The y coordinates of atoms are given and the directions of the a, b and c axes provide orientation

The chains of tetrahedra extending parallel to (010) account for the perfect cleavage parallel to this plane. The natural material from Alamos occurs in the form of aggregates of prismatic radiating fibers with individual fibers elongated parallel to [010], and it is natural to expect the occurrence of a major structural unit in this direction. The Pb atoms provide a continuous spiraling chain of edge-sharing polyhedra in this direction which is illustrated in Fig. 2. The coordination polyhedra of Pb(1)-Pb(3) are defined by the six oxygen atoms O(5)-O(10). The atoms Pb(1), O(6) and O(10) are approximately coplanar, with nearly equal y coordinates. Similarly, the sets of atoms Pb(2), O(8), O(9) and Pb(3), O(5), O(7) are coplanar and each set varies in level by about 1/3 y. They are thus related by an approximation to a 3₁ screw axis located parallel to [010] between Pb(1), Pb(2) and Pb(3). If the Pb(1)-O(8) bond (2.89Å) is included in the Pb(1) coordination polyhedron, each Pb polyhedron may be considered to share an edge with the Pb polyhedra above and below it, and related to it by the pseudo-screw. In this way a continuous spiral of Pb-O bonds extends parallel to [010]. The nature of the Pb-O bonding thus further differentiates the alamosite structure from those of the pyroxenes and pyroxenoids whose relations are primarily determined through ionic-bonding relations within a close-packed anion frame.